Độ sáng thực tế (luminosity) – lượng bức xạ thoát ra của một ngôi sao trên một đơn vị thời gian – là một đặc tính nội tại của ngôi sao. Độ sáng này không phụ thuộc vào bất kỳ vị trí cũng như sự di chuyển nào của người quan sát ngôi sao. Độ sáng này được tham chiếu từ độ sáng tuyệt đối (absolute brightness) của một ngôi sao. Tuy nhiên, khi chúng ta quan sát một ngôi sao, chúng ta không nhìn thấy độ sáng tuyệt đối của chúng mà nhìn thấy độ sáng biểu kiến (apparent brightness).
Độ sáng biểu kiến của một vật thể là độ sáng của một vật thể đối với người quan sát, phụ thuộc vào cả độ sáng thực tế của vật thể, phụ thuộc vào khoảng cách giữa vật thể và người quan sát và cũng phụ thuộc vào bất kỳ sự hấp thụ ánh sáng nào dọc theo đường đi từ vật thể đến người quan sát.
Định luật bình phương nghịch đảo (Inverse-Square Law)
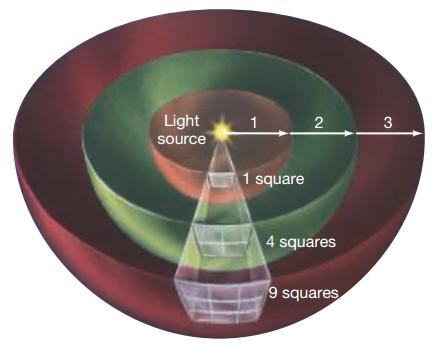
Hình 1. Định luật bình phương nghịch đảo: Khi ánh sáng di chuyển ra khỏi một nguồn sáng (chẳng hạn như một ngôi sao), nó yếu dần đi khi lan rộng trên các bề mặt diện tích lớn dần (biểu thị ở đây là các phần của vỏ hình cầu). Do đó, lượng bức xạ nhận được từ một máy dò (độ sáng biểu kiến của nguồn sáng) tỷ lệ nghịch với bình phương khoảng cách của máy dò đến nguồn sáng.
Hình 1 cho thấy ánh sáng thoát ra từ một ngôi sao và di chuyển vào không gian. Chuyển động ra ngoài, bức xạ đi qua các mặt cầu tưởng tượng có bán kính tăng dần bao quanh nguồn. Tia sáng truyền đi càng xa nguồn thì năng lượng truyền qua mỗi đơn vị diện tích càng ít. Bởi vì diện tích của mặt cầu tăng chính bằng bình phương bán kính của mặt cầu tăng (S = 4πR2), nên năng lượng trên một diện tích hay độ sáng biểu kiến của một ngôi sao tỷ lệ nghịch với bình phương khoảng cách từ ngôi sao đến người quan sát.
Tăng gấp đôi khoảng cách từ một ngôi sao sẽ khiến cho ngôi sao mờ đi 22 = 4 lần. Tăng gấp ba lần khoảng cách sẽ làm giảm độ sáng đi 32 = 9 lần, v.v…
Dĩ nhiên, độ sáng tuyệt đối của một ngôi sao cũng ảnh hưởng đến độ sáng biểu kiến của nó. Gấp đôi độ sáng tuyệt đối bằng gấp đôi năng lượng vượt qua các lớp vỏ cầu bao quanh ngôi sao và do đó gấp đôi độ sáng biểu kiến. Độ sáng biểu kiến của một ngôi sao tỷ lệ thuận với độ sáng tuyệt đối của ngôi sao và tỷ lệ nghịch với bình phương khoảng cách từ người quan sát đến ngôi sao:
độ sáng biểu kiến ∞ độ sáng thực tế / khoảng cách2
(Lưu ý: ∞ là ký hiệu cho sự tỷ lệ).
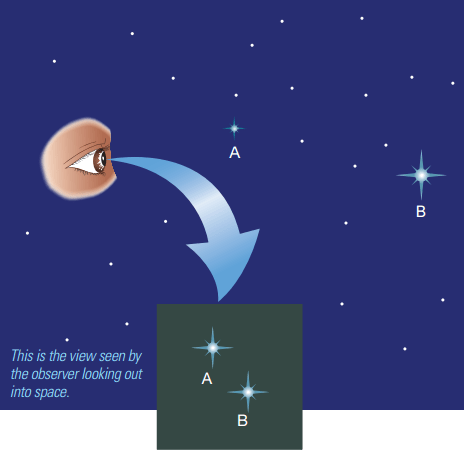
Hình 2 Độ sáng tuyệt đối
Hai ngôi sao A và B có độ sáng tuyệt đối khác nhau, chúng có thể xuất hiện với độ sáng bằng nhau đối với một người quan sát từ Trái Đất.
Nếu như ngôi sao B sáng hơn thì ngôi sao B ở xa hơn ngôi sao A. Vì vậy, hai ngôi sao giống hệt nhau có thể có cùng độ sáng biểu kiến khi và chỉ khi chúng cùng cách xa Trái Đất một khoảng cách bằng nhau.
Tuy nhiên, như hình minh họa 2, hai ngôi sao không giống nhau cũng có thể có cùng độ sáng biểu kiến nếu như ngôi sao có độ sáng thực tế lớn hơn nằm xa hơn.
Nếu ta nhìn thấy một ngôi sao sáng thì hoặc nó phát ra bức xạ mạnh hoặc nó nằm gần Trái Đất hoặc cả hai. Và tương tự, khi ta nhìn thấy một ngôi sao mờ nhạt nghĩa là ngôi sao đó phát ra bức xạ yếu hoặc ở xa Trái Đất hoặc cả hai.
Điểm lại kiến thức: Độ sáng thực tế và độ sáng biểu kiến
Nếu vẫn còn gặp khó khăn trong việc áp dụng định luật nghịch đảo bình phương khi thảo luận về độ sáng biểu kiến của các ngôi sao thì hãy ghi nhớ một vài điểm trọng tâm sau:
– Độ sáng biểu kiến của một ngôi sao tỷ lệ thuận với độ sáng thực tế của nó (đo mức phát xạ năng lượng thực của nó). Độ sáng thực tế tăng gấp đôi thì độ sáng biểu kiến tăng gấp đôi.
– Độ sáng biểu kiến của một ngôi sao tỷ lệ nghịch với bình phương khoảng cách. Khoảng cách tăng gấp đôi thì độ sáng biểu kiến giảm đi bốn lần.
– Nếu hai ngôi sao xuất hiện với độ sáng nhìn thấy bằng nhau, ngôi sao nào có độ sáng thực tế yếu hơn thì hẳn nó ở gần hơn và cũng như vậy với ngôi sao kia.
Vậy công việc xác định độ sáng thực tế của một ngôi sao chỉ là công việc tỷ lệ. Đầu tiên, nhà thiên văn học phải xác định được độ sáng biểu kiến của ngôi sao bằng cách đo lượng năng lượng được phát hiện qua kính thiên văn trong một khoảng thời gian nhất định. Sau đó, khoảng cách của ngôi sao phải được đo bằng phương pháp thị sai đối với các ngôi sao ở gần và bằng các phương tiện khác cho các ngôi sao ở xa hơn. Và sau đó, ta dùng định luật nghịch đảo bình phương để tìm độ sáng thực tế.
Thang đo cường độ (The magnitude scale)
Thay vì đo độ sáng biểu kiến bằng đơn vị SI (độ sáng được đo bằng joules mỗi giây hoặc watts trên bình phương khoảng cách, chính là W/m2), để thuận tiện hơn thì các nhà thiên văn – quang học họ sẽ làm việc với thang độ lớn (xếp hạng các ngôi sao theo độ sáng biểu kiến của chúng).
Thang đo cường độ này có từ thế kỷ II TCN, khi nhà thiên văn học Hy Lạp Hipparchus dùng mắt thường phân chia các ngôi sao thành sáu mức sáng. Ông đã phân loại các ngôi sao sáng nhất ở cấp 1, các ngôi sao sáng tiếp theo ở cấp 2, và cứ thế tiếp tục đến những ngôi sao mờ nhất, tối nhất có thể nhìn thấy bằng mắt thường ở cấp 6. Cấp 1 (sáng nhất) đến cấp 6 (mờ nhất) thống kê các ngôi sao được người xưa biết đến. Theo quy ước như vậy thì ngôi sao chúng ta nhìn thấy càng sáng thì lớn ứng với cấp sao biểu kiến càng bé và ngược lại.

Năm 1856, Norman Robert Pogson chuẩn hóa hệ thống này, phát hiện ra hai sự thật quan trọng về thang đo độ lớn:
- Thứ nhất, một ngôi sao ở cấp 1 có độ sáng biểu kiến sáng hơn khoảng 100 lần một ngôi sao ở cấp 6 trong thang đo cường độ của Hipparchus.
- Thứ hai, hai sao có cấp sao khác nhau một cấp có độ sáng biểu kiến khác nhau 2,5 lần. Nói cách khác, đối với mắt người, ngôi sao cấp 1 sáng hơn ngôi sao cấp 2 khoảng 2,5 lần; ngôi sao thứ 2 sáng hơn ngôi sao thứ 3 khoảng 2,5 lần; tiếp tục như vậy cho các cấp sao tiếp theo.
Và thật đúng như vậy, hai sao ở cấp 1 và cấp 6 cách nhau năm cấp có độ sáng biểu kiến khác nhau 100 lần, vậy hai sao có cấp sao khác nhau một cấp có độ rọi khác nhau = 2,512 lần.

Hình 3. Cường độ biểu kiến: Biểu đồ minh họa cường độ biểu kiến của một vài vật thể thiên văn, giới hạn ở vật thể mờ nhất chúng ta tìm thấy được nhờ các kính thiên văn chuyên dụng để quan sát chúng.
Bởi vì chúng ta đang dùng mắt thường quan sát các sao rồi xếp vào bảng phân cấp của Hipparchus nên các nhà thiên văn học gọi đây là thang đo độ sáng biểu kiến. Nhưng chúng ta có một phiên bản hiện đại của thang đo độ sáng biểu kiến xác định rằng hai sao cách nhau năm cấp có độ sáng biểu kiến khác nhau 100 lần.
Ngoài ra, hệ thống hiện đại không còn giới hạn ở các số nguyên và đã mở rộng hơn ngoài 6 cấp biểu. Có các sao có cường độ nằm ngoài cấp 1 đến cấp 6.
Các thiên thể rất sáng có cấp sao nhỏ hơn 1 và các vật thể rất mờ có cấp sao lớn hơn 6. Hình 3 minh họa độ sáng biểu kiến của một số thiên thể từ Mặt Trời (-26,7) đến vật thể mờ nhất có thể đo được bằng kính viễn vọng Hubble hoặc Keck có độ sáng biểu kiến là +30 – khi nhìn từ khoảng cách bằng đường kính Trái Đất có thể tưởng tượng nó mờ như một con đom đóm.
Cường độ biểu kiến (apparent magnitude) đo độ sáng biểu kiến (apparent brightness) của một ngôi sao khi chúng ta nhìn thấy ở một khoảng cách thực từ ngôi sao đến chúng ta. Tuy nhiên, để so sánh các đặc tính nội tại chính là độ sáng tuyệt đối của các ngôi sao, các nhà thiên văn học bèn tưởng tượng họ đang nhìn vào các ngôi sao ở một khoảng cách tiêu chuẩn là 10pc.
Cách sử dụng khoảng cách tiêu chuẩn là 10pc này đã giúp họ thuận tiện hơn rất nhiều.
Và từ đó, cường độ tuyệt đối (absolute magnitude) của một thiên thể được định nghĩa là độ sáng biểu kiến của thiên thể đó khi quan sát ở khoảng cách 10pc. Và với định nghĩa như vậy, khoảng cách là cố định, cường độ tuyệt đối là thước đo độ sáng thực tế của một ngôi sao.
Mặc dù Mặt Trời có cường độ biểu kiến là một số âm (-26,7 – có nghĩa là rất sáng trên bầu trời) nhưng khi di chuyển Mặt Trời đến khoảng cách 10pc so với Trái Đất thì độ sáng lúc này là độ sáng tuyệt đối còn 4,8 – tức là nó chỉ sáng hơn một chút so với các ngôi sao mờ nhất có thể thấy trên bầu trời đêm. Độ lớn tuyệt đối tương đương với độ sáng thực tế – một đặc tính nội tại của một ngôi sao.
Cho cường độ tuyệt đối của Mặt Trời là 4,8; chúng ta có thể xây dựng bảng chuyển đổi (trong hình bên cạnh) giữa hai đại lượng này.
Khi giảm cấp sao xuống 5 cấp chính là tăng độ sáng lên 100 lần.
Vậy một ngôi sao sáng gấp 100 lần Mặt Trời có độ sáng thực tế là 4,8 − 5 = −0,2
Ngôi sao có độ sáng yếu hơn độ sáng Mặt Trời 100 lần có độ sáng tuyệt đối là 4,8 + 5 = 9,8.
Chúng ta có thể điền vào bảng chuyển đổi với cấp 1 bằng
≈ 2,512, cấp 2 có cường độ bằng
≈ 6,310 và tiếp tục như vậy. Hệ số 10 tương ứng với cường độ 2,5.
Bạn có thể sử dụng bảng này để chuyển đổi giữa độ sáng thực tế của Mặt Trời sáng cường độ tuyệt đối.
Theo định luật nghịch đảo bình phương, nếu tăng khoảng cách tới một ngôi sao 10 lần thì độ sáng biểu kiến giảm đi 100 lần, do đó làm tăng cấp sao biểu kiến lên 5 đơn vị. Tương tự, tăng khoảng cách lên 100 lần làm tăng cấp sao biểu kiến lên 10 đơn vị, v.v…. Vậy, mỗi lần tăng khoảng cách lên hệ số 10 thì cấp sao tăng 5. Vì độ sáng tuyệt đối là độ sáng biểu kiến ở khoảng cách 10 pc, chúng ta có thể viết:
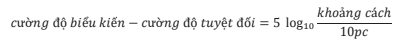
Mặc dù không giống với định luật nghịch đảo bình phương, nhưng hai phương trình này là tương đương với nhau.
Đối với các ngôi sao cách Trái Đất hơn 10pc, cường độ biểu kiến lớn hơn cường độ tuyệt đối. Với các ngôi sao gần hơn 10pc thì ngược lại. Ví dụ, Mặt Trời với cường độ tuyệt đối bằng 4,8; khi nhìn Mặt Trời từ khoảng cách 100pc có cường độ biểu kiến bằng: 4,8 + 5 log10 100 = 14,8. Độ sáng này yếu hơn rất nhiều so với ngưỡng nhìn thấy của ống nhòm hay kính thiên văn.
Ngôi sao Rigel Kentaurus (còn được gọi là Alpha Centauri) có cường độ tuyệt đối +4,34 và được quan sát với độ sáng biểu kiến là -0,01. Nó cách nhau -4,35, do đó khoảng cách của ngôi sao đó đến Trái Đất bằng 10pc × 10−4,34/5 = 1,35pc bằng với kết quả thu được nhờ phương pháp thị sai.
Tham khảo:
Sách Astronomy a beginner’s guide to the universe.
Được tổng hợp và chia sẻ bởi Ái Linh, Văn Luận, Thị Hồng, Văn Duy – Ban Học Thuật
Biên tập bởi Nguyễn Gia Khanh – Ban Truyền Thông




Bình luận